Bitmap Index和在Druid中的应用
Bitmap Index(位图索引)广泛应用于很多大数据分析系统中, 如Druid, Kylin等, 是一种高效的索引技术. 尤其是Druid中将Bitmap替换为Roaring Bitmap, 到底是什么东西呢?
基本概念
何为Bitmap
Bitmap中文为位图, (Java中是BitSet类), 是指用一连串的01bit位来表示一个”整数set”. eg:
- 整数数组: [3,4,6,8,10,12,13,14,15]
- bitmap: 0001 1010 1010 1111
面试题: 有一个超大的整数数组, 里面存放的是范围0-20亿的integer, 设计一个方法能够快速判断给定的一个数是否在这个数组中.
答案: 创建一个Bitmap, 对于数组中每个整数(如42), 将bitmap对应位(如第42个bit)置为1. 这样给定一个数, 只有看对应bit为是否为1即可判断.
(为了统一语言, 在上图bitmap中我们从左向右看, 即第0个bit位在最左)
何为Bitmap Index
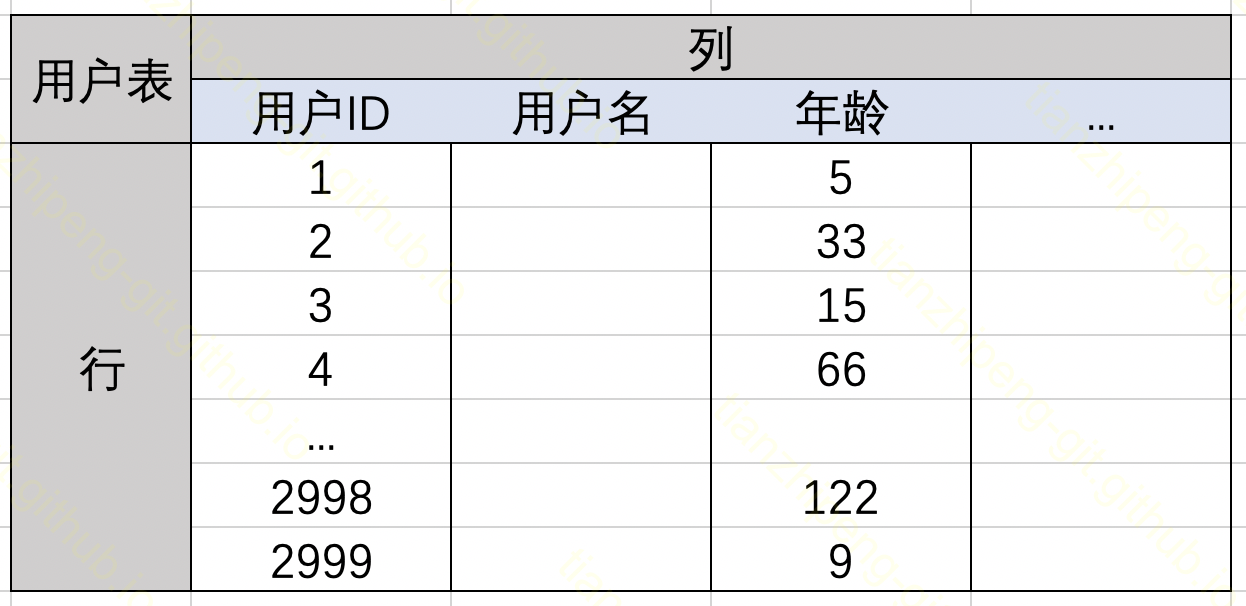 图1.
图1.
先看如图所示的原始数据. 我们经常处理的一般都是这种表格式的数据, 如果要对年龄这一列做一个索引便于快速查找, 传统方法都是建一个B树类的索引. 那借助Bitmap结构实现的位图索引是什么样的呢?
最简单款Bitmap Index如下图:
- 对于年龄这一列的每一个可能的取值, 创建一个bitmap
- 某个bitmap的第x个bit位为1, 代表对应用户id为x的用户的年龄是这个bitmap对应的年龄.
- (所以bitmap的长度要大于等于用户id的最大值)
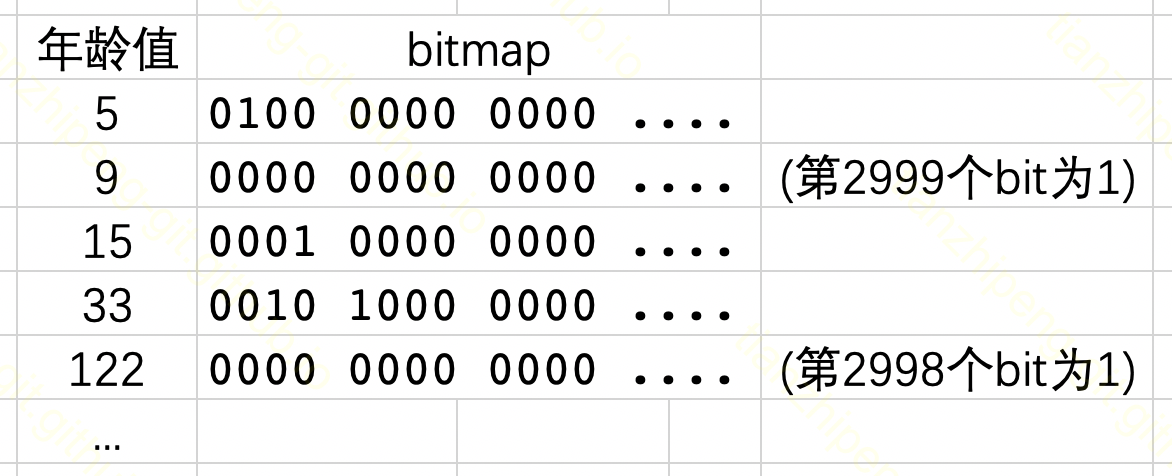 图2.
图2.
Bitmap索引的优势和缺点
如上图的Bitmap Index中, 有如下优势:
where age = 33等值条件的查询: 只需要读取年龄33这一个bitmap, 找到所有值为1的位置, 就是年龄33的用户id.where age = 33 or age = 5带逻辑运算的查询: 只需要将对应值的bitmap取出, 把多个bitmap进行对应的逻辑运算即可. 如将33和5两个bitmap进行并(逻辑或)运算, 结果bitmap中所有值为1的就是要查询的用户id.where age > 33范围查询: 因为年龄值我们可以排好了序, 所以把值>33的所有年龄bitmap取出做或运算即可 (有可能某个范围的值太多, 要进行或运算太多, 效率不高)where age = 33 and gender = male多个列的组合查询: 只要两个列都建了bitmap index, 也可以进行逻辑运算. (这种可以对多个查询条件进行逻辑运算的功能, 是B树这类索引做不到的)- 需要的存储空间相对小, 尤其是应用了后文提到的压缩bitmap的方法后.
缺点:
- 对经常变动更新的数据不友好
- 如果该列的基数很大, 会导致bitmap数量很多
文本如何索引
实际情况中, 我们要索引的列大多不是年龄这种数字, 而是字符串/文本, 这时候如果用Bitmap索引, 就需要先做一些事:
- 分词: 可选步骤, 将原始字符串进行各类分词, 不分词的话只能按照完整字符串值才能索引到. 如”computer science”可分词为”computer”, “science”. (或者进一步分为”co”, “com”, “comp”, “compu” … 参看N-Gram分词)
- 字典表: 分词之后的字符串, 放入一个字典表进行编号, 这样字符串就变为整数序号了.
- bitmap: 进行正常的Bitmap索引
 图3.
图3.
压缩Bitmap索引
我们回头看图2这个5行N位的bitmap index, 当列(年龄)的基数很大, 要索引的记录数(用户id)也很大的时候, 存储空间占用就会比较高, 如何有效的压缩Bitmap索引, 又能保证上面提到的Bitmap索引的优势不丢失呢?
我将压缩方法分为纵向和横向两类(各类论文里习惯分为binning/encoding/compression三类)
纵向压缩 binning/encoding
纵向压缩bitmap索引, 就是使用各种方法减少bitmap的个数.
- binning是通过分桶, 减少要编码的key的个数(减少年龄值)
- encoding是指如何将列值编码为bitmap index的左侧的序号, 决定了有多少个bitmap. 常见的encoding有
range encoding,inerval encoding和下面讲的binnary encoding
binning分桶
分桶是指将原始的列值按一定范围分为桶, 对桶进行索引而不是原始值.
比如年龄这一列. 我们可以定0-10岁, 11-20岁等每10岁为一桶, 将原始的各个年龄放入桶中, 那么0-130岁的范围不管有多少个年龄值, 都只需要13个bitmap即可.
这种方案很简单, 缺点也很明显, 它丢失了原始值的信息, 对某些范围查询还能立即返回, 但没法准确回答age=33这种查询的结果了, 只能知道31-40这个桶有哪些用户id, 然后去原始数据中判断这些用户中有哪些真的是等于33岁.
所以这种方案实际中不怎么使用.
binnary encoding
binnary encoding的bitmap index, 也叫做bit-slice index. 对于上面提到bitmap index例子, 我们观察列值, 也就是年龄的值, 我们发现年龄值最大也就是几百, 那么对年龄值的个位十位百位, binnary encoding方法形成30个bitmap:

用法示例:
- 原始用户id为1的年龄是5岁, 那么在这30个bitmap中,
- 个位的第5个bitmap的第1位标记为1.
- 十位的第0个bitmap的第1位标记为1.
- 百位的第0个bitmap的第1位标记为1.
- 原始用户id为2998的年龄是122岁, 那么在这30个bitmap中,
- 个位的第2个bitmap的第2998位标记为1.
- 十位的第2个bitmap的第2998位标记为1.
- 百位的第1个bitmap的第2998位标记为1.
- (图中的bit标志和文字描述不一样, 只是示意)
这样用30个bitmap就解决了原始最多1000个bitmap的事情, 空间当然节省了. 当需要查询age=33的用户时, 只要把 个位第3个bitmap, 十位第3个bitmap, 百位第0个bitmap 这3个bitmap取出, 做一个且操作, 得到的结果bitmap中就是年龄33岁的用户id.
当然实际应用中不可能用10进制这么呆的设定, 而是用2进制, 也就是bit位来拆分. 比如年龄最大是200岁, 最大值也不超过8个bit(256), 所以根据二进制拆分, 用8个bitmap就可以搞定了.
实际使用中在上面的简单款binary encoding中加入了其他设定, 如notnull值bitmap, 加入range等.
以上提到的所以encoding方案, 都没法处理一个列有多个值的情况.
横向压缩 compress
横向压缩bitmap index, 其实就是对单个bitmap的bit位进行压缩.
WAH和Concise
对单个bitmap进行压缩, 最常用的一个算法思想是RLE(Run Length Encoding), 就是指: 如果有连续100个bit位的值都是0, 存储100,0两个数字比存储100个bit更划算.
WAH就是一种利用RLE思想设计的方案. 全称word-aligned hybrid code. 从全称中可以看出WAH压缩格式是一种字对齐的混合结构.
WAH压缩的内部格式的最小单元是字(一般一个字就是32个bit). WAH的的字有两种情况, 原文字(literal word)和压缩字(fill word).
- 两种字通过32个bit中的第一个bit来区分, 第一个bit为0是原文字, 为1则是压缩字.
- 如果是原文字, 那么这个字剩余的31个bit, 和原始bitmap中未压缩的31个bit一模一样.
- 如果是压缩字, 那么剩余31个bit中:
- 第2bit表示压缩的值是0还是1
- 剩余30个bit表示有多少字的重复的值, 称为run number.
- 比如第一个bit是1, 第2个bit是1, 剩下30个bit是数值5, 则表示有
连续的5*31个1. (这就是RLE的地方)
 图4.
图4.
图中:
- 第四行是WAH压缩后的字s, 用16进制表示的
- 第一行是原始bitmap情况, 1个1, 20个0, 3个1 …
- 第二行是原始bitmap, 按31个bit为一组
- 第三行是第二行的16进制表示
这样对照第四行看:
- 第一个字, 40000380, 第一个bit是0则表示是原文字(4=0100), 所以这个字之后的31个字节正是原始bitmap的内容, 即: 1个1, 20个0, 3个1, 7个0(共31bit).
- 第二个字, 80000002, 第一个bit是1则表示是压缩字(8=1000), 第二个bit是0表示压缩的值是0, 后面30个bit的数值是2, 则表示连续2*31个0, 正是原始bitmap对应的62个0.
- 第三个和第四个字, 都是原文字, 不再分析.
Concise
WAH算法比较简单且有效, 之后有很多变种, Concise就是其中之一, Concise也是Druid最开始采用的bitmap压缩算法.
Concise方法的提出是观察到很多这样的情况, 非常稀疏的bitmap, 有着连续非常多的0, 中间只偶尔出现几个1, WAH算法对于这种情况, 每个1的地方都要被迫采用原文字, 不能压缩了.
在Concise中, 原文字和WAH一样, 压缩字的设计有所不同:
- 压缩字中, 除了第一个bit表示字的类型, 第二个bit表示压缩的值, 还要拿出5个git(即log(32))来, 作为position位, 剩余的25个bit的数值才用来表示重复次数(run number)
- 那中间留出来的5个position位的数值(能表示0-31), 表示这个压缩字对应的原始bitmap中前31个bit, 有一位需要翻转.
- 举例来说, Concise中的压缩字: 00 00011 0000…100 的含义是:
- 是个压缩字, 压缩的值是0, 有’连续’
4*31个0, 但是其中第3个bit其实要翻转为1
可能看起来也没多好, 但论文说在某些场景下比WAH多压缩50%空间呢…
Roaring Bitmap
Druid的新版本中已经将Bitmap压缩算法切换为Roaring, 这个算法也被很多其他大数据分析系统所采用. Roaring Bitmap被证明在多数情况下优于其他压缩方法, 可以作为默认Bitmap方案.
讲Roaring Bitmap之前, 我们要先摆脱bitmap是一堆0011的思想, 回到文章开头提到的bitmap本质, 一个integer set, 能快速判断一个integer是否存在的set.
原始bitmap可能有无限长, 这里我们先简化为, 要压缩的bitmap最长就是40亿个bit. 里面包含的都是一个unsigned int能表示的正整数. eg:
- 示例数组:
[3,8,10,333, 678, 60000, 72343], 比如里面是用户id. - 这个integer set如果用bitmap表示, 就是第3位是1, 第8位是1, 第10位是1 …
- 之后本节我们考虑的东西都是这个integer set
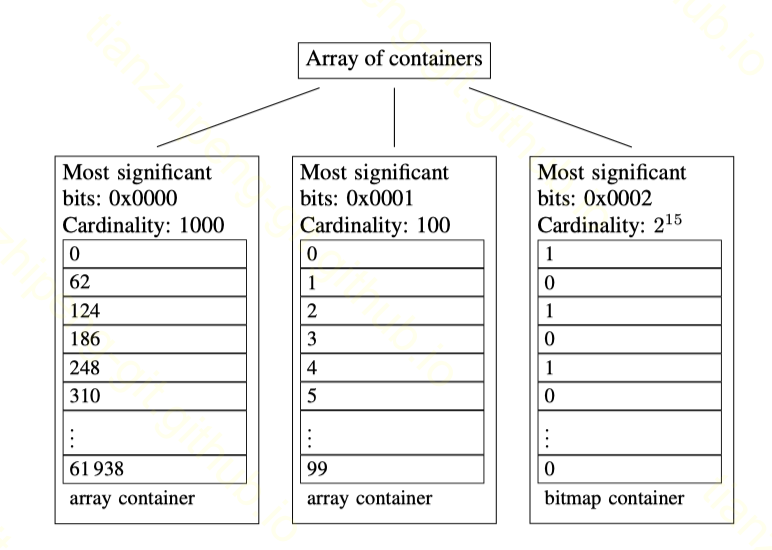
Roaring Bitmap内部是两层结构:
第一层:
- 首先将刚才提到的unsigned int的0-40亿范围, 分为65536个chunk, 那么每个chunk负责的65536个integer (6万*6万=40亿 或 16+16=32 😁)
- 第一层结构就是长度最大为65536的数组, 就对应上面的chunk. 长这样: [e0, e1, e2, … e65535]. (初始为空, 随着数据加入增加元素)
- 那么对于integer set中的每个数(就是bitmap中的每个1), 除以65536就可以得到它应该在这个数组的哪个槽中.(除以65536的结果, 本质上是这个integer的前16位bit/most significant 16 bits)
- 比如上面示例数组中前面的元素都落在第一个槽, 最后一个72343落在第二个槽.
第二层:
上面数组中每个元素我写的e0, e1, 具体是什么东西呢? 数据中的元素其实叫container, 一共有三种container, ArrayContainer, BitmapContainer, RunContainer.
①
初始情况下, 默认为槽上创建一个ArrayContainer, 内部就是一个数组, 将实际数值除65536取模的值放入其中. (除65536取模的结果用一个short, 即16bit即可表示, 其本质上是这个integer的后16位)
比如示例数组[3,8,10,333, 678, 60000, 72343], 前面的元素除65536都是0, 即落在数组第一个槽e1中, e1目前是一个ArrayContainer, 就把这些元素除65536的余数放入ArrayContainer. 72343落在第二个槽, e2目前也上一个ArrayContainer, 就把6870(即72343%65536)放入e2中.
②
当ArrayContainer中的integer过多(超过4096个)的时候, 就将ArrayContainer转化为BitmapContainer. BitmapContainer内部就是一个66536长度的基本bitmap, 然后用基本bitmap的方案将integer们标记出来.
这个不做任何压缩的BitmapContainer的长度固定是65536. 而ArrayContainer中如果存了4096个元素, 4096*16=65536, 这时候转化为BitmapContainer更加划算.
③
第三种Container叫RunContainer, 就是用了RLE的Bitmap, 它不是在数据插入时自动转化的, 而是所有数据插入完后, 进行一波判断, 要不要将ArrayContainer和BitmapContainer转化为RunContainer.
要不要转化的判断标准当然也是空间上划不划算, 其实就是计算一个Container中有多少个连续的段(称为run), 当run的数量较多时就转化为RunContainer.
这个RunContainer虽然也是RLE, 但是表示方法和WAH的不同, 它内部也是一个short数组, 如[11, 4, 25, 2 …], 两个一对, 表示从第11个bit开始连续4位是1, 从第25个bit开始连续两位是1.
整体看Roaring就是这样一种两层的混合结构. (这种根据数量动态决定结构的思想像不像HashMap)
Bitmap Index in Druid
- Druid中默认为每个维度列创建Bitmap索引, 都是先做字典在做bitmap
- segment文件中对于每列, 包含一个字典, 一个原值list, 一个bitmap list.
- 没有使用任何纵向的压缩技术/encoding, 就是一个值一个bitmap
本来以为Bitmap和Druid的结合能有一些内容, 结果Druid就是最简单的使用了RoaringBitmap而已..
More
只是概述的讲了bitmap概念和几种算法, 其实相关的内容很多. 比如我忽略了很多其实挺有意思的点:
- 如上各类的bitmap和压缩方案的生成算法.
- 如上各类的bitmap和压缩方案中, 压缩之后如何进行各种条件查询, 如何进行各类逻辑运算的算法.
Reference
参考基本都是论文:
- Druid:
- Optimizing Druid with Roaring bitmaps
- Druid - A Real-time Analytical Data Store
- The anatomy of a Druid segment file
- encoding
- Improved Query Performance with Variant Indexes
- Multi-level and Multi-component Bitmap Encoding for Efficient Search Operations
- Using Bitmaps to Perform Range Queries - Pilosa
- compress
- Concise: Compressed ’n’ Composable Integer Set (Concise)
- Better bitmap performance with Roaring bitmaps
- Consistently faster and smaller compressed bitmaps with Roaring
- A Survey of Bitmap Index Compression Algorithms for Big Data
- Compressing Bitmap Indexes for Faster Search Operations (WAH)
